בינה מאלכותית RB108-3 – מבוא לרשתות ניירונים ובינה מלאכותית

חלק א:

העשרה : נתחיל משהו מצחיק – מזכיר SUNO

2 .notebooklm פודקאסט

קישור ל-NotebookLM: https://notebooklm.google/

מה יכולת ה-NotebookLM

מה אפשר להעלות?

קבצים: PDF, Google Docs, Google Slides. Google Help+2datacamp.com+2
קישורים לאתרים או YouTube עם כתוביות. datacamp.com+1
ערכי טקסט-גולמיים שהדבקת באופן ידני. datacamp.com

מה המערכת יודעת לעשות?

ליצור סיכומים אוטומטיים של המקורות. Google NotebookLM+2datacamp.com+2
מענה לשאלות בשפה טבעית בהתבסס על המקורות שהועלו, עם ציטוטים מדויקים. datacamp.com+1
הפקת “Audio Overviews” (סיכום אודיו) ו-“Video Overviews” (הצגת וידאו/מצגות) מתוך התוכן שלך. blog.google+2Google Help+2
יצירת כלי עזר נוספים: Mind Maps, Study Guides, Flashcards, Quizzes. Workspace Updates Blog+1
שיתוף מחברות (Notebooks) עם אחרים, ניתוח שימוש, הרשאות משתנות. Google Help

איך ניתן שהיא לא תוסיף דברים שלא בחורנו ?

היא עובדת כ-RAG (Retrieval Augmented Generation): כלומר, התשובות מבוססות בעיקר על המקורות שהעלית. arXiv+1
בכל תשובה מופיעים ציטוטים שמצביעים על המקור המדויק שבו המידע לקוח. datacamp.com+1
חשוב לוודא שהמקורות עצמם אמינים, עדכניים ומלאים — איכות המקורות משפיעה ישירות על האמינות. datacamp.com
אם אין מקור מתאים, יש להיזהר: המערכת עדיין עלולה “להשליך” מידע שלא מגובה. למשל במחקר נמצא שיעור “hallucinations” נמוך יותר מ-LLMים רגילים אך לא אפסי. arXiv+1

איך היא כן תוסיף עצמה – תכנים אוטומטיים

עם העלאת המקורות, המערכת יכולה לייצר אוטומטית סיכומים, שאלות מוצעות, ואף Audio/Video Overviews ללא פקודה מפורשת. Google Help
ניתן לבחור לשנות שפה/פורמט של הפלט (למשל לשפות שונות או פורמטים שונים) ולהתאים את הפלט לקהל או למטרה
“הוסף מידע חיצוני אם חסר” → היא תשלב מקורות כלליים.

אפשרות “Auto-Expand”

בממשק החדש (2025) יש כפתור “Expand with Gemini” שמאפשר להוסיף תובנות והרחבות מעבר למידע שבמחברת.
אם לוחצים עליו, NotebookLM מבצעת הרחבה באמצעות מודל השפה, תוך שמירת ההבחנה בין ציטוטים מהמקורות לבין השלמות AI.

אם זאת יש לעבור אחרי המידע שהיא אספה לעומק

חלק ב: פיתוח מוצר בעזרת בינה מלאכותית LLM

תרגיל כיתה 1 : פיתוח מוצר בצורה מדעית והנדסית – מזווית מדעית תאורטית (תרגיל חובה)

בנה בעזרת בינה מלאכותית מערכת אשר עשויה לזהות מצלמה נסתרת בגודל 10 ממ אשר משמת בעיקר במצלמות רוורס
איזה אפשריות קיימות בשוק ומה מחירים
איזה מודל פיסקאלי ומדעי מאפשר לזהות את המצלמות
כיצד ניתן לסרוק חדר , לזיהוי המצלמה איזה תדרים חסרונות ויתרונות
חפש סרטונים בנושא : על פי מה עובדים הסרטונים הקיימים
בנה טבלת השוואה , על הבטלה לעשות טבלת השוואה בין השיטות (עיקרון מדעי , מחיר , אמינות )
בקש מאמרים מדעים וקישור למאמרים מדעיים
כיצד אתה יודע שהבינה מלאכותית לא טועה ? הוכח זאת !

חלק ג : מבוא רשתות נוירונים (ראשוני)

רשתות ניירונים ANN בינה מלאכותית

מעבר בין שכבות	יש פונקציית אקטיבציה?	איפה היא מיושמת בפועל	הערה קצרה

קלט → חבויה

כן (בדרך כלל)

אחרי החישוב הלינארי של השכבה החבויה:

$z=Wx+b$ $z = W x + b$ ואז

$a=f(z)$ $a = f (z)$

שכבת הקלט עצמה בלי אקטיבציה

חבויה → חבויה

כן (בדרך כלל)

אחרי

$Wx+b$ $W x + b$ בכל שכבה חבויה

לרוב ReLU וכו’

חבויה → פלט

תלוי במשימה

או אחרי

$Wx+b$ $W x + b$ בשכבת הפלט, או בתוך ה-loss (עם logits)

רגרסיה: לרוב בלי; בינארי: sigmoid; רב־מחלקתי: softmax

פונקציה אקטיבציה : (פועלת על כל ניירון בודד )

פונקציית אקטיבציה היא החלק ברשת שמכניס “אי־לינאריות”.

בלי אקטיבציה, גם אם שמים הרבה שכבות Dense, כל הרשת תישאר בסוף חיבור של פעולות לינאריות, כלומר תתנהג כמו נוסחה לינארית אחת גדולה. במצב כזה הרשת יכולה ללמוד טוב רק קשרים פשוטים (כמו קו ישר), אבל מתקשה ללמוד עקומות מורכבות, תנאים, “אם-אז”, גבולות, ותבניות לא לינאריות.

2. שימוש כמתג : שפעול הניירון נוספת להבין אקטיבציה היא כ”מתג” על כל נוירון. כל נוירון מחשב קודם ערך פנימי:

$z = Wx + b$

$z = W x + b$

ואז האקטיבציה מחליטה מה ייצא קדימה:

$a = f(z)$

$a = f (z)$

במובן אינטואיטיבי, היא יכולה להפעיל נוירון (להעביר ערך משמעותי), או לכבות אותו (להחזיר 0 או ערך קטן), וכך נוצרת התנהגות של “שערים” שמדלקים/מכבים חלקים מהרשת לפי הקלט. לדוגמה, ReLU עושה בדיוק דבר כזה: אם

$z<0$

$z < 0$ היא מחזירה 0 (כיבוי), ואם

$z>0$

$z > 0$ היא מעבירה את

$z$

$z$ (הפעלה). זה מאפשר לרשת לבנות פונקציות מורכבות מחלקים, כאילו יש אוסף של “כללים” שמופעלים רק כשצריך.

בנוסף, האקטיבציה עוזרת לרשת להתמודד עם אי־רציפויות או התנהגות “עם פינות” בעולם האמיתי. הרבה תופעות נראות כמו פונקציה שבקטעים שונים מתנהגת אחרת (למשל: עד סף מסוים אין תגובה, ואז יש תגובה חזקה; או מערכת שמתנהגת אחרת מעל/מתחת לערך קריטי). אקטיבציות כמו ReLU ומשפחתה יוצרות פונקציות שהן “חתוכות לקטעים” (piecewise), עם נקודות מעבר חדות יחסית, ולכן הן מסוגלות לבנות קירוב טוב גם לפונקציות שיש בהן שינוי חד בהתנהגות. חשוב לדייק: רשת סטנדרטית בדרך כלל תלמד קירוב רציף לפונקציה, אבל היא יכולה לייצר מעבר חד מאוד שנראה כמעט לא רציף, וכך להתאים לנתונים שמציגים “קפיצות” או שינוי פתאומי.

למה יש הרבה סוגי אקטיבציות? כי כל סוג נותן “אופי” אחר:

יש כאלה שמקלות על אימון עמוק ויציב (לכן ReLU/LeakyReLU/GELU נפוצות בשכבות חבויות).
יש כאלה שמגבילות פלט לטווח מסוים (למשל Sigmoid ל־0..1 כשצריך הסתברות).
יש כאלה שמתאימות לסיווג רב־מחלקתי (Softmax כדי לקבל הסתברויות שסכומן 1).
וחלק נבחרות כדי לשפר זרימת גרדיאנטים ולהימנע מבעיות באימון (כמו גרדיאנט נעלם).

בשורה אחת: פונקציית אקטיבציה מוסיפה אי־לינאריות, מאפשרת “הדלקה/כיבוי” של נוירונים לפי הקלט, ועוזרת לרשת לבנות פונקציות מורכבות עם אזורים שונים והתנהגות חדה, כולל קירוב טוב למצבים שנראים כמעט לא־רציפים.

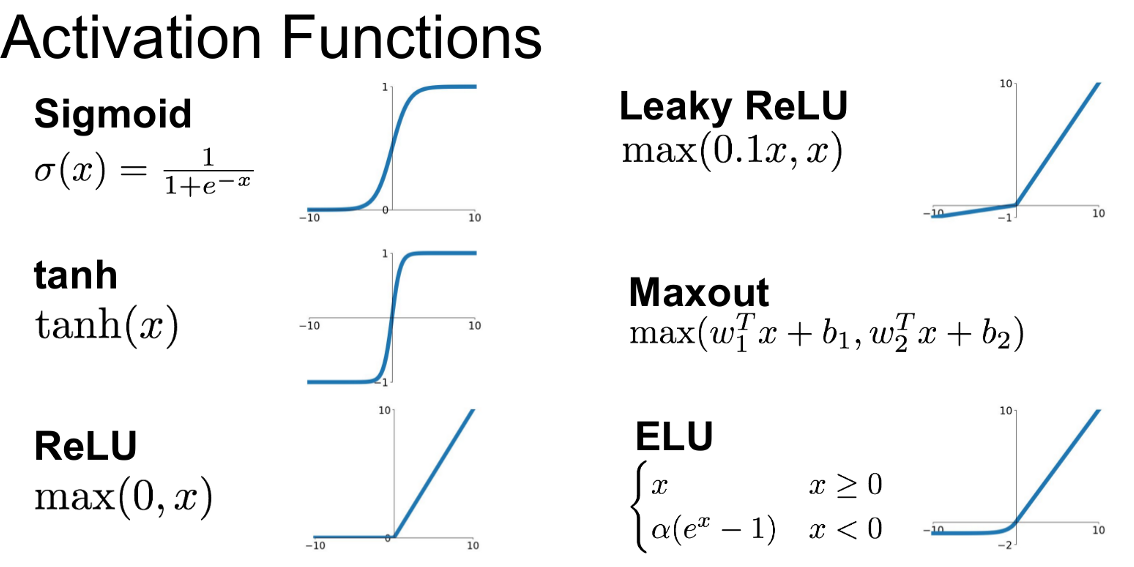
טבלת מושגים בסיסית :

Concept	Meaning (in this code)	Where you see it	Example from your program
Input (features)	The numbers you feed into the model so it can learn the rule	`x = np.linspace(...)` and `model.Input(shape=(1,))`	`x` values between -2 and 2 (one feature per sample)
Output / Target (labels)	The “correct answer” the model should learn to predict from `x`	`y = 3x5 - 5x*2 + 2x + 14`	`y` is the true function value for each `x`
Model Output (prediction)	What the network actually predicts for a given input	`predicted = model.predict(x_test)`	`predicted[i][0]` is the predicted `y` for `x_test[i]`
Activation function	A non-linear function applied after a Dense layer’s linear part (`Wx+b`) to let the network learn complex shapes	`Dense(..., activation='relu')`	`relu(z)=max(0,z)` used in the hidden layers
Linear part (Wx + b)	The weighted sum + bias computed inside each Dense layer before activation	inside every `Dense(...)`	Not written explicitly; Keras does it internally
Hidden layer	Internal layers that transform input step-by-step before final output	`Dense(64, activation='relu')`	3 hidden layers with 64 neurons each
Output layer	Last layer that produces the final numeric prediction	`Dense(1)`	1 neuron, no activation (linear), good for regression
Loss (error measure)	How wrong the model is; training tries to minimize it	`loss='mean_squared_error'` and `loss_log`	MSE: average of `(y_true - y_pred)^2`
Epoch	One full pass of training over all training samples	`epochs = 760` and the training loop	Each loop iteration trains 1 epoch (`epochs=1`)

הסבר איזה סוג רשת

import tensorflow as tf                       # TensorFlow + Keras (build/train neural networks)
import numpy as np                            # Numerical arrays and math
import matplotlib.pyplot as plt               # Plotting graphs
import pandas as pd                           # Data tables (used in the commented loss-table section)
from tensorflow.keras.utils import plot_model  # Utility to visualize the model (not used below)

# Step 1: Training data  # y = 2x + 1
x = np.array([0, 1, 2, 3, 4, 10], dtype=float)   # Inputs (features). Added x=10 as an extra training point
y = np.array([1, 3, 5, 7, 9, 21], dtype=float)   # Targets (labels). For x=10, y=21 (still y=2x+1)

# Step 2: Build model
model = tf.keras.Sequential([                 # Sequential = stack layers in order
    tf.keras.Input(shape=(1,)),               # Input layer: each sample has 1 feature; shape=(1,)
    tf.keras.layers.Dense(10, activation='relu'), # Hidden layer 1:
                                                  # units=10 neurons, activation='relu' applies non-linearity
    tf.keras.layers.Dense(12, activation='relu'), # Hidden layer 2:
                                                  # units=12 neurons, activation='relu'
    tf.keras.layers.Dense(10, activation='relu'), # Hidden layer 3:
                                                  # units=10 neurons, activation='relu'
    tf.keras.layers.Dense(1)                  # Output layer:
                                              # units=1 for regression; no activation => linear output
])

# Step 3: Compile model
model.compile(
    optimizer='adam',                         # Optimizer: Adam (adaptive learning-rate gradient descent)
    loss='mean_squared_error'                 # Loss: MSE for regression (squared prediction error)
)

# Step 4: Train model and collect loss manually
loss_log = []                                 # Store loss values per epoch for plotting
epochs = 350                                  # Number of epochs (passes over the dataset)

for epoch in range(epochs):                   # Manual epoch loop to log loss each epoch
    history = model.fit(
        x, y,                                 # Training inputs and targets
        epochs=1,                             # Train one epoch per loop iteration
        verbose=0                             # 0=silent, 1=progress bar, 2=one line per epoch
    )
    loss = history.history['loss'][0]         # Extract the loss for this epoch
    loss_log.append(loss)                     # Save loss value
    print(f"Epoch {epoch+1:03d}: loss = {loss:.6f}")  # Print epoch count and loss

# Step 5: Predict multiple values
x_test = np.array([3.0, 4.0, 8.0])            # Test inputs to evaluate generalization (includes x=8 not in training)
predicted = model.predict(x_test)             # Predict outputs; returns shape (N, 1)

print("\nPredictions:")
for i, val in enumerate(x_test):              # Loop over test inputs
    print(f"x = {val:.1f} → y ≈ {predicted[i][0]:.4f}")  # predicted[i][0] extracts scalar from (1,) vector

# Step 6: Show internal layer outputs manually for x = 3.0 (COMMENTED OUT)
# x_input = tf.constant([[3.0]])              # Tensor input with shape (1,1) to match model input
# print("\nManual Layer Outputs for x = 3.0:")
# layer_input = x_input                       # Start with the input tensor
# for i, layer in enumerate(model.layers):    # Iterate through model layers
#     layer_output = layer(layer_input)       # Forward pass through this layer
#     print(f"Layer {i+1} ({layer.name}) output:\n{layer_output.numpy()}\n")
#     layer_input = layer_output              # Feed output to the next layer

# Step 7: Show full loss table (COMMENTED OUT)
# loss_df = pd.DataFrame({                    # Build a table of epoch and loss
#     'Epoch': np.arange(1, epochs+1),        # Epoch numbers 1..epochs
#     'Loss': loss_log                        # Loss values collected above
# })
# print("\n=== Final Epoch Loss Table ===")
# print(loss_df.to_string(index=False))       # Print the loss table

# Step 8: Plot
plt.figure(figsize=(10, 4))                   # Figure size in inches: (width, height)

# Plot 1: Model fit and predictions
plt.subplot(1, 2, 1)                          # Subplot grid: 1 row, 2 columns, select subplot #1
plt.scatter(x, y, label='Training Data')      # Training points (x,y)
plt.plot(x, model.predict(x), color='red', label='Model Fit')  # Model predictions on training x
plt.scatter(x_test, predicted, color='orange', label='Predictions x=3,4,8') # Predicted test points
plt.legend()                                  # Show legend
plt.xlabel("x")                               # X-axis label
plt.ylabel("y")                               # Y-axis label
plt.title("Model Fit and Predictions")        # Plot title

# Plot 2: Loss curve
plt.subplot(1, 2, 2)                          # Subplot grid: 1 row, 2 columns, select subplot #2
plt.plot(loss_log)                            # Loss vs epoch index (0..epochs-1)
plt.title("Training Loss Over Epochs")        # Plot title
plt.xlabel("Epoch")                           # X-axis label
plt.ylabel("Loss")                            # Y-axis label
plt.grid(True)                                # Add grid

plt.tight_layout()                            # Adjust spacing to prevent overlap
plt.show()                                    # Display the figure

import tensorflow as tf # TensorFlow + Keras (build/train neural networks)

import numpy as np # Numerical arrays and math

import matplotlib.pyplot as plt # Plotting graphs

import pandas as pd # Data tables (used in the commented loss-table section)

from tensorflow.keras.utils import plot_model # Utility to visualize the model (not used below)

# Step 1: Training data # y = 2x + 1

x = np.array([0, 1, 2, 3, 4, 10], dtype=float) # Inputs (features). Added x=10 as an extra training point

y = np.array([1, 3, 5, 7, 9, 21], dtype=float) # Targets (labels). For x=10, y=21 (still y=2x+1)

# Step 2: Build model

model = tf.keras.Sequential([ # Sequential = stack layers in order

tf.keras.Input(shape=(1,)), # Input layer: each sample has 1 feature; shape=(1,)

tf.keras.layers.Dense(10, activation='relu'), # Hidden layer 1:

# units=10 neurons, activation='relu' applies non-linearity

tf.keras.layers.Dense(12, activation='relu'), # Hidden layer 2:

# units=12 neurons, activation='relu'

tf.keras.layers.Dense(10, activation='relu'), # Hidden layer 3:

# units=10 neurons, activation='relu'

tf.keras.layers.Dense(1) # Output layer:

# units=1 for regression; no activation => linear output

])

# Step 3: Compile model

model.compile(

optimizer='adam', # Optimizer: Adam (adaptive learning-rate gradient descent)

loss='mean_squared_error' # Loss: MSE for regression (squared prediction error)

)

# Step 4: Train model and collect loss manually

loss_log = [] # Store loss values per epoch for plotting

epochs = 350 # Number of epochs (passes over the dataset)

for epoch in range(epochs): # Manual epoch loop to log loss each epoch

history = model.fit(

x, y, # Training inputs and targets

epochs=1, # Train one epoch per loop iteration

verbose=0 # 0=silent, 1=progress bar, 2=one line per epoch

)

loss = history.history['loss'][0] # Extract the loss for this epoch

loss_log.append(loss) # Save loss value

print(f"Epoch {epoch+1:03d}: loss = {loss:.6f}") # Print epoch count and loss

# Step 5: Predict multiple values

x_test = np.array([3.0, 4.0, 8.0]) # Test inputs to evaluate generalization (includes x=8 not in training)

predicted = model.predict(x_test) # Predict outputs; returns shape (N, 1)

print("\nPredictions:")

for i, val in enumerate(x_test): # Loop over test inputs

print(f"x = {val:.1f} → y ≈ {predicted[i][0]:.4f}") # predicted[i][0] extracts scalar from (1,) vector

# Step 6: Show internal layer outputs manually for x = 3.0 (COMMENTED OUT)

# x_input = tf.constant([[3.0]]) # Tensor input with shape (1,1) to match model input

# print("\nManual Layer Outputs for x = 3.0:")

# layer_input = x_input # Start with the input tensor

# for i, layer in enumerate(model.layers): # Iterate through model layers

# layer_output = layer(layer_input) # Forward pass through this layer

# print(f"Layer {i+1} ({layer.name}) output:\n{layer_output.numpy()}\n")

# layer_input = layer_output # Feed output to the next layer

# Step 7: Show full loss table (COMMENTED OUT)

# loss_df = pd.DataFrame({ # Build a table of epoch and loss

# 'Epoch': np.arange(1, epochs+1), # Epoch numbers 1..epochs

# 'Loss': loss_log # Loss values collected above

# })

# print("\n=== Final Epoch Loss Table ===")

# print(loss_df.to_string(index=False)) # Print the loss table

# Step 8: Plot

plt.figure(figsize=(10, 4)) # Figure size in inches: (width, height)

# Plot 1: Model fit and predictions

plt.subplot(1, 2, 1) # Subplot grid: 1 row, 2 columns, select subplot #1

plt.scatter(x, y, label='Training Data') # Training points (x,y)

plt.plot(x, model.predict(x), color='red', label='Model Fit') # Model predictions on training x

plt.scatter(x_test, predicted, color='orange', label='Predictions x=3,4,8') # Predicted test points

plt.legend() # Show legend

plt.xlabel("x") # X-axis label

plt.ylabel("y") # Y-axis label

plt.title("Model Fit and Predictions") # Plot title

# Plot 2: Loss curve

plt.subplot(1, 2, 2) # Subplot grid: 1 row, 2 columns, select subplot #2

plt.plot(loss_log) # Loss vs epoch index (0..epochs-1)

plt.title("Training Loss Over Epochs") # Plot title

plt.xlabel("Epoch") # X-axis label

plt.ylabel("Loss") # Y-axis label

plt.grid(True) # Add grid

plt.tight_layout() # Adjust spacing to prevent overlap

plt.show() # Display the figure

הסבר על הקוד מבנה רשת ומושגי יסוד

MLP (Multi-Layer Perceptron) הוא סוג רשת עצבית “קדימה” (Feed-Forward) שמורכבת משכבות Dense / Fully-Connected. מטרת הרשת היא ללמוד מיפוי בין קלט לפלט:

$x \rightarrow \hat{y}$

$x \to y^$

כאשר

$\hat{y}$

$y^$ הוא החיזוי שהרשת מחזירה.

1) מה זה MLP

MLP היא רשת שבה:

המידע זורם רק קדימה: קלט → שכבות חבויות → פלט.
כל שכבה היא Dense: כל נוירון מחובר לכל הערכים שיוצאים מהשכבה הקודמת.
בדרך כלל יש פונקציית אקטיבציה בשכבות החבויות כדי לאפשר לרשת ללמוד קשרים לא-לינאריים.

2) קלט (Input) ותכונות (Features)

Input / Features הם הנתונים שהרשת מקבלת כדי לבצע חיזוי.

בדוגמה:

x = np.array([0,1,2,3,4,10])

כאן לכל דוגמה יש תכונה אחת בלבד (מספר אחד). לכן במודל מופיע:

tf.keras.Input(shape=(1,))

המשמעות של shape=(1,):

כל דוגמה היא וקטור באורך 1:

$[x]$ $[x]$
אם לכל דוגמה היו 3 תכונות (למשל

$x_1,x_2,x_3$ $x_{1}, x_{2}, x_{3}$ ), היה נכתב shape=(3,).

3) פלט יעד (Targets / Labels)

Targets (Labels) הם “התשובות הנכונות” שהרשת צריכה ללמוד לחזות.

בדוגמה:

y = np.array([1,3,5,7,9,21])

כל זוג

$(x,y)$

$(x, y)$ הוא דוגמת אימון:

$x=0 \Rightarrow y=1$

$x = 0 \Rightarrow y = 1$
$x=10 \Rightarrow y=21$

$x = 10 \Rightarrow y = 21$

המטרה באימון היא לגרום לכך שכאשר הרשת תקבל

$x$

$x$ , היא תחזיר

$\hat{y}$

$y^$ קרוב ל-

$y$

$y$ .

4) נוירון (Neuron) ומה הוא מחשב

בשכבת Dense, כל נוירון מבצע שני שלבים:

שלב א: חישוב לינארי

$z = W x + b$

$W$

$W$ = משקולות (Weights)
$b$

$b$ = הטיה (Bias)
$x$

$x$ = הקלט לשכבה (וקטור)
$z$

$z$ = פלט לפני אקטיבציה (נקרא גם pre-activation)

שלב ב: אקטיבציה (Activation)

$a = f(z)$

$a = f (z)$

$f$

$f$ = פונקציית אקטיבציה
$a$

$a$ = הפלט של הנוירון אחרי האקטיבציה

בקוד לא רואים את

$W$

$W$ ו-

$b$

$b$ נכתבים מפורש, אבל הם קיימים בכל Dense(...) ונלמדים במהלך האימון.

5) שכבת Dense / Fully-Connected

שכבת Dense עם units = N אומרת:

יש N נוירונים בשכבה.
כל אחד מה-N מקבל את כל הערכים מהשכבה הקודמת.

בדוגמה:

Dense(10, relu) → 10 נוירונים
Dense(12, relu) → 12 נוירונים
Dense(10, relu) → 10 נוירונים
Dense(1) → נוירון אחד בפלט

6) שכבות חבויות (Hidden Layers)

שכבות חבויות הן השכבות בין הקלט לפלט. הן “מעבדות” את הקלט בשלבים.

בדוגמה:

3 שכבות חבויות: 10 → 12 → 10

למה צריך שכבות חבויות?

כדי ללמוד פונקציות מורכבות.
עם זאת, במקרה של

$y=2x+1$ $y = 2 x + 1$ מדובר בקשר לינארי, ולכן אפשר גם מודל פשוט יותר (למשל שכבת Dense(1) אחת).

7) פונקציית אקטיבציה (Activation Function)

ללא אקטיבציה, גם אם יש כמה שכבות Dense, הרשת נשארת בסופו של דבר לינארית.
כדי ללמוד קשרים לא-לינאריים (עקומות מורכבות) חייבים אקטיבציה.

בדוגמה האקטיבציה היא:

activation='relu'

ReLU

$\text{ReLU}(z) = \max(0, z)$

$ReLU (z) = max (0, z)$

מה היא עושה:

אם

$z$ $z$ שלילי → יוצא 0
אם

$z$ $z$ חיובי → נשאר כמו שהוא

8) שכבת פלט (Output Layer) וסוג הבעיה (Regression)

שכבת הפלט בדוגמה:

Dense(1) בלי אקטיבציה

זה מתאים ל-Regression (רגרסיה): ניבוי מספר רציף.

למה בלי אקטיבציה בפלט?

כי ברגרסיה רוצים שהפלט יוכל להיות כל מספר (לא מוגבל ל-0..1 או להסתברות).

9) פונקציית הפסד (Loss) – MSE

הפסד (Loss) מודד כמה החיזוי שגוי. כאן משתמשים ב:

mean_squared_error (MSE)

$\text{MSE} = \frac{1}{N}\sum (y – \hat{y})^2$

$MSE = N 1 \sum (y - y^)^{2}$

ככל שה-MSE קטן יותר, החיזוי קרוב יותר לערכים האמיתיים.

10) אופטימייזר (Optimizer) – Adam

האופטימייזר הוא האלגוריתם שמעדכן את

$W$

$W$ ו-

$b$

$b$ כדי להקטין את ה-Loss.

בדוגמה:

optimizer='adam'

Adam הוא וריאציה יעילה של Gradient Descent עם התאמת קצב למידה לכל פרמטר.

11) Epoch ואימון (Training)

Epoch הוא מעבר אימון אחד על כל הדאטה.

בדוגמה:

epochs = 350
בתוך הלולאה: model.fit(..., epochs=1)

כל איטרציה בלולאה מאמנת Epoch אחד, שומרת Loss, ומדפיסה אותו.

12) חיזוי (Prediction) והכללה (Generalization)

אחרי אימון, הרשת מבצעת חיזוי באמצעות:

model.predict(x_test)

בדוגמה:

x_test = [3.0, 4.0, 8.0]

הערך 8 לא נמצא בדאטה המקורי (0,1,2,3,4,10), ולכן הוא בודק יכולת הכללה: ללמוד את הכלל ולא רק לזכור נקודות.

קישור :

https://colab.research.google.com/drive/1aS5y_LKPePjloHi57PZforMGqOESZGgX?usp=sharing

4. ,תרגיל כיתה : בניית רשת ניירונים בעזרת בינה מלאוכתית

4.1 בנה בעזרת בינה מלאוכתי רשת ניירונים בקוד פייטון – בסביבת פיתוח קולאב אשר מקבל את הנתונים הבאים

4.2 הצג את גרף הלימודה הפעל על 40 איפוקס , 100 איפוקס האם הרשת למדה או דרוש יותר ?

4.3 נבא את התוצאות : הבאות

0.1 , 1.5 . -2.85 , 2.6

4.4 הצג את גרף הנתונים של סידרה a ואת הערכים לניסוי

נתונים ערכים לשאלה :

a = [
    (0, 2107.063993),
    (1, 1774.894936),
    (2, 1750.009562),
    (3, 1481.326385),
    (4, 1396.077521),
    (5, 1206.241582),
    (6, 1226.093311),
    (7, 1053.402700),
    (8, 863.965419),
    (9, 708.908089),
    (10, 609.188688),
    (11, 507.225962),
    (12, 546.267593),
    (13, 527.910129),
    (14, 445.411797),
    (15, 372.281130),
    (16, 273.318001),
    (17, 232.070553),
    (18, 162.902607),
    (19, 135.674182),
    (20, 15.810602),
    (21, 32.953371),
    (22, -7.529706),
    (23, -58.090834),
    (24, 141.533792),
    (25, 14.234175),
    (26, 40.625799),
    (27, -59.885817),
    (28, 86.203475),
    (29, 31.991252),
    (30, 88.132789),
    (31, 160.413156),
    (32, -75.607018),
    (33, 55.269403),
    (34, -56.520119),
    (35, -94.585288),
    (36, 8.086607),
    (37, -69.322549),
    (38, 81.048572),
    (39, 35.469407),
    (40, 13.428026),
    (41, 55.077948),
    (42, -76.633790),
    (43, 15.156530),
    (44, -100.269949),
    (45, 82.102218),
    (46, -39.703165),
    (47, -12.988640),
    (48, -82.648318),
    (49, -174.654761),
    (50, -125.680074),
    (51, 114.949028),
    (52, 2.739873),
    (53, 51.751231),
    (54, 8.351202),
    (55, -29.036185),
    (56, -138.659365),
    (57, 45.099863),
    (58, 4.898423),
    (59, -140.341615),
    (60, 0.263349),
    (61, -171.835728),
    (62, -112.363502),
    (63, 8.291108),
    (64, 42.170526),
    (65, -95.476512),
    (66, 89.265808),
    (67, 121.477131),
    (68, 63.346685),
    (69, 22.926077),
    (70, -54.681239),
    (71, -0.003649),
    (72, -58.438858),
    (73, 56.850423),
    (74, -62.948579),
    (75, 88.712425),
    (76, -139.472977),
    (77, -32.893119),
    (78, 11.448258),
    (79, -38.987336),
    (80, 25.303369),
    (81, -81.415682),
    (82, -70.917732),
    (83, 24.433327),
    (84, 10.738649),
    (85, -96.212815),
    (86, -14.961291),
    (87, -92.290469),
    (88, -104.987551),
    (89, 15.086477),
    (90, -118.130072),
    (91, -72.749843),
    (92, -172.149650),
    (93, -118.275654),
    (94, -57.536845),
    (95, 37.355310),
    (96, -174.049250),
    (97, 67.392092),
    (98, -178.348884),
    (99, 32.446615),
    (100, 34.355661),
    (101, -29.564107),
    (102, -230.259215),
    (103, -18.166889),
    (104, -186.462794),
    (105, -81.414764),
    (106, -287.880945),
    (107, -140.773498),
    (108, -300.851027),
    (109, -378.673102),
    (110, -492.544540),
    (111, -547.831068),
    (112, -489.163215),
    (113, -822.436100),
    (114, -742.851594),
    (115, -925.768624),
    (116, -885.407152),
    (117, -1112.968628),
    (118, -1234.314197),
    (119, -1212.259426),
    (120, -1629.306669),
    (121, -1508.318170),
    (122, -1887.185332),
    (123, -2070.217978),
]

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

a = [

(0, 2107.063993),

(1, 1774.894936),

(2, 1750.009562),

(3, 1481.326385),

(4, 1396.077521),

(5, 1206.241582),

(6, 1226.093311),

(7, 1053.402700),

(8, 863.965419),

(9, 708.908089),

(10, 609.188688),

(11, 507.225962),

(12, 546.267593),

(13, 527.910129),

(14, 445.411797),

(15, 372.281130),

(16, 273.318001),

(17, 232.070553),

(18, 162.902607),

(19, 135.674182),

(20, 15.810602),

(21, 32.953371),

(22, -7.529706),

(23, -58.090834),

(24, 141.533792),

(25, 14.234175),

(26, 40.625799),

(27, -59.885817),

(28, 86.203475),

(29, 31.991252),

(30, 88.132789),

(31, 160.413156),

(32, -75.607018),

(33, 55.269403),

(34, -56.520119),

(35, -94.585288),

(36, 8.086607),

(37, -69.322549),

(38, 81.048572),

(39, 35.469407),

(40, 13.428026),

(41, 55.077948),

(42, -76.633790),

(43, 15.156530),

(44, -100.269949),

(45, 82.102218),

(46, -39.703165),

(47, -12.988640),

(48, -82.648318),

(49, -174.654761),

(50, -125.680074),

(51, 114.949028),

(52, 2.739873),

(53, 51.751231),

(54, 8.351202),

(55, -29.036185),

(56, -138.659365),

(57, 45.099863),

(58, 4.898423),

(59, -140.341615),

(60, 0.263349),

(61, -171.835728),

(62, -112.363502),

(63, 8.291108),

(64, 42.170526),

(65, -95.476512),

(66, 89.265808),

(67, 121.477131),

(68, 63.346685),

(69, 22.926077),

(70, -54.681239),

(71, -0.003649),

(72, -58.438858),

(73, 56.850423),

(74, -62.948579),

(75, 88.712425),

(76, -139.472977),

(77, -32.893119),

(78, 11.448258),

(79, -38.987336),

(80, 25.303369),

(81, -81.415682),

(82, -70.917732),

(83, 24.433327),

(84, 10.738649),

(85, -96.212815),

(86, -14.961291),

(87, -92.290469),

(88, -104.987551),

(89, 15.086477),

(90, -118.130072),

(91, -72.749843),

(92, -172.149650),

(93, -118.275654),

(94, -57.536845),

(95, 37.355310),

(96, -174.049250),

(97, 67.392092),

(98, -178.348884),

(99, 32.446615),

(100, 34.355661),

(101, -29.564107),

(102, -230.259215),

(103, -18.166889),

(104, -186.462794),

(105, -81.414764),

(106, -287.880945),

(107, -140.773498),

(108, -300.851027),

(109, -378.673102),

(110, -492.544540),

(111, -547.831068),

(112, -489.163215),

(113, -822.436100),

(114, -742.851594),

(115, -925.768624),

(116, -885.407152),

(117, -1112.968628),

(118, -1234.314197),

(119, -1212.259426),

(120, -1629.306669),

(121, -1508.318170),

(122, -1887.185332),

(123, -2070.217978),

]

רשתות ניירונים ANN בינה מלאכותית

הרשת שבה השתמשנו היא רשת מסוג Classification (סיווג), כלומר – רשת שנועדה לבחור בין כמה אפשרויות ולהחליט לאיזו קטגוריה שייך הקלט. במקרה שלנו, הרשת מקבלת מיקום של נקודה במרחב (שני ערכים: X ו־Y) ומסווגת אותה לאחת משלוש קבוצות: אדום, ירוק או כחול.

רשת כזו שייכת למשפחת הרשתות העצביות המלאכותיות (Artificial Neural Networks), ובפרט – לרשתות מסוג Dense Feedforward, שבהן כל נוירון בשכבה אחת מחובר לכל הנוירונים בשכבה הבאה. הרשת מתבססת על למידה מפוקחת (Supervised Learning) – כלומר, היא לומדת מדוגמאות מתויגות מראש.

במה היא שונה מרשת שחוזה ערך כמו טמפרטורה?

רשת שמטרתה לחזות טמפרטורה (או כל ערך מספרי אחר) נקראת Regression Network (רשת רגרסיה). במקום לבחור קטגוריה, היא מנבאת ערך רציף אחד, למשל: 21.4 מעלות.

הבדל עיקרי בין סיווג לרגרסיה:

Classification – הפלט הוא אחת מתוך קבוצה סופית של אפשרויות (למשל: אדום, ירוק או כחול) , זהוי מילה שהוקלטה , קטגוריה של המוצר , קטגוריה של התקלה , האם האדם קופץ הולך , נופל מתגלגל .
הפלט ברשת סיווג הוא לרוב וקטור של הסתברויות לכל קטגוריה, והרשת בוחרת את ההסתברות הגבוהה ביותר.

Regression – הפלט הוא מספר ממשי אחד מתוך טווח בלתי מוגבל (למשל: חיזוי מחיר של מוצר, טמפרטורה , גובה , לחץ של תמיסה).
רגרסיה הפלט הוא פשוט מספר אחד – פלט אחד

קישור ל ANN – (Artificial Neural Network) classifier

https://colab.research.google.com/drive/1MgFjPa8y-megnslGQ7-lhqqxPeKlwype?usp=sharing

SDR – Software Defined Radio

SDRA2021 Talks: Electrosense, Neural Network Signal Classification, gr-rpitx, Radio Astronomy and More

RF Training Data Generation for Machine Learning

Automatic Identification of 160 Shortwave RF Signals with Deep Learning

תרגיל כיתה 2.1 רשת ניירונים חיזוי קטגוריה

המטרה של הרשת היא ללמוד לזהות, על בסיס מיקום, לאיזו קבוצה צבעונית משתייכת נקודה חדשה.

במערכת שלנו, רשת הנוירונים לומדת לסווג נקודות במרחב לפי מיקומן. כל נקודה מורכבת משני מספרים – מיקום בציר האופקי (X) ובציר האנכי (Y).
זהו הקלט: שני מספרים שמייצגים את מיקום הנקודה.

הפלט הוא הסיווג שהרשת נותנת לנקודה – האם היא שייכת לקבוצת אדום, ירוק או כחול. הרשת מחליטה לפי מה שלמדה מהנתונים הקודמים.

מטרה :

import numpy as np
import matplotlib.pyplot as plt

# Re-create data
np.random.seed(42)
red = np.random.normal(loc=[2, 2], scale=0.5, size=(100, 2))
green = np.random.normal(loc=[5, 5], scale=0.5, size=(100, 2))
blue = np.random.normal(loc=[8, 2], scale=0.5, size=(100, 2))

# Plot each group
plt.figure(figsize=(7, 5))

plt.scatter(red[:, 0], red[:, 1], color='red', label='Red Group', alpha=0.7)
plt.scatter(green[:, 0], green[:, 1], color='green', label='Green Group', alpha=0.7)
plt.scatter(blue[:, 0], blue[:, 1], color='blue', label='Blue Group', alpha=0.7)

plt.title('Color Group Clusters (2D)')
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.grid(True)
plt.show()

import numpy as np

import matplotlib.pyplot as plt

# Re-create data

np.random.seed(42)

red = np.random.normal(loc=[2, 2], scale=0.5, size=(100, 2))

green = np.random.normal(loc=[5, 5], scale=0.5, size=(100, 2))

blue = np.random.normal(loc=[8, 2], scale=0.5, size=(100, 2))

# Plot each group

plt.figure(figsize=(7, 5))

plt.scatter(red[:, 0], red[:, 1], color='red', label='Red Group', alpha=0.7)

plt.scatter(green[:, 0], green[:, 1], color='green', label='Green Group', alpha=0.7)

plt.scatter(blue[:, 0], blue[:, 1], color='blue', label='Blue Group', alpha=0.7)

plt.title('Color Group Clusters (2D)')

plt.xlabel('X1')

plt.ylabel('X2')

plt.legend()

plt.grid(True)

plt.show()

import numpy as np
import matplotlib.pyplot as plt

# Re-create data
np.random.seed(42)
red = np.random.normal(loc=[2, 2], scale=1.8, size=(100, 2))
green = np.random.normal(loc=[5, 5], scale=1.8, size=(100, 2))
blue = np.random.normal(loc=[8, 2], scale=1.8, size=(100, 2))

# Plot each group
plt.figure(figsize=(7, 5))

plt.scatter(red[:, 0], red[:, 1], color='red', label='Red Group', alpha=0.7)
plt.scatter(green[:, 0], green[:, 1], color='green', label='Green Group', alpha=0.7)
plt.scatter(blue[:, 0], blue[:, 1], color='blue', label='Blue Group', alpha=0.7)

plt.title('Color Group Clusters (2D)')
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.grid(True)
plt.show()

import numpy as np

import matplotlib.pyplot as plt

# Re-create data

np.random.seed(42)

red = np.random.normal(loc=[2, 2], scale=1.8, size=(100, 2))

green = np.random.normal(loc=[5, 5], scale=1.8, size=(100, 2))

blue = np.random.normal(loc=[8, 2], scale=1.8, size=(100, 2))

# Plot each group

plt.figure(figsize=(7, 5))

plt.scatter(red[:, 0], red[:, 1], color='red', label='Red Group', alpha=0.7)

plt.scatter(green[:, 0], green[:, 1], color='green', label='Green Group', alpha=0.7)

plt.scatter(blue[:, 0], blue[:, 1], color='blue', label='Blue Group', alpha=0.7)

plt.title('Color Group Clusters (2D)')

plt.xlabel('X1')

plt.ylabel('X2')

plt.legend()

plt.grid(True)

plt.show()

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from tensorflow.keras.utils import to_categorical

# Create synthetic data (3 clusters)
np.random.seed(42)
red = np.random.normal(loc=[2, 2], scale=1.8, size=(100, 2))
green = np.random.normal(loc=[5, 5], scale=1.8, size=(100, 2))
blue = np.random.normal(loc=[8, 2], scale=1.8, size=(100, 2))

# Combine the data and labels
X = np.vstack((red, green, blue))
y = np.array(['R'] * 100 + ['G'] * 100 + ['B'] * 100)

# Encode labels
encoder = LabelEncoder()
y_encoded = encoder.fit_transform(y)
y_categorical = to_categorical(y_encoded)

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y_categorical, test_size=0.2, random_state=42)

# Build the model
model = tf.keras.Sequential([
    tf.keras.layers.Input(shape=(2,)),
    tf.keras.layers.Dense(16, activation='relu'),
    tf.keras.layers.Dense(12, activation='relu'),
    tf.keras.layers.Dense(3, activation='softmax')  # 3 output classes
])

# Compile the model
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

# Train the model (increased epochs)
history = model.fit(X_train, y_train, epochs=150, batch_size=16, validation_data=(X_test, y_test))

# Plot training history
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], label='Train Loss', color='red')
plt.plot(history.history['val_loss'], label='Val Loss', color='orange')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Model Loss over Epochs')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(history.history['accuracy'], label='Train Accuracy', color='blue')
plt.plot(history.history['val_accuracy'], label='Val Accuracy', color='green')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('Model Accuracy over Epochs')
plt.legend()

plt.tight_layout()
plt.show()

# ---------------------
# 🔍 Prediction Examples
# ---------------------
test_points = np.array([
    [1, 1],     # Likely Red
    [5, 5],     # Likely Green
    [9, 1.5],   # Likely Blue
    [4, 4],     # Maybe Green
    [7, 2.5]    # Maybe Blue
])

preds = model.predict(test_points)
pred_labels = encoder.inverse_transform(np.argmax(preds, axis=1))

print("\nPrediction Examples:")
for point, label in zip(test_points, pred_labels):
    print(f"Point {point} → Predicted Color: {label}")

import numpy as np

import matplotlib.pyplot as plt

import tensorflow as tf

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import LabelEncoder

from tensorflow.keras.utils import to_categorical

# Create synthetic data (3 clusters)

np.random.seed(42)

red = np.random.normal(loc=[2, 2], scale=1.8, size=(100, 2))

green = np.random.normal(loc=[5, 5], scale=1.8, size=(100, 2))

blue = np.random.normal(loc=[8, 2], scale=1.8, size=(100, 2))

# Combine the data and labels

X = np.vstack((red, green, blue))

y = np.array(['R'] * 100 + ['G'] * 100 + ['B'] * 100)

# Encode labels

encoder = LabelEncoder()

y_encoded = encoder.fit_transform(y)

y_categorical = to_categorical(y_encoded)

# Split data

X_train, X_test, y_train, y_test = train_test_split(X, y_categorical, test_size=0.2, random_state=42)

# Build the model

model = tf.keras.Sequential([

tf.keras.layers.Input(shape=(2,)),

tf.keras.layers.Dense(16, activation='relu'),

tf.keras.layers.Dense(12, activation='relu'),

tf.keras.layers.Dense(3, activation='softmax') # 3 output classes

])

# Compile the model

model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

# Train the model (increased epochs)

history = model.fit(X_train, y_train, epochs=150, batch_size=16, validation_data=(X_test, y_test))

# Plot training history

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)

plt.plot(history.history['loss'], label='Train Loss', color='red')

plt.plot(history.history['val_loss'], label='Val Loss', color='orange')

plt.xlabel('Epoch')

plt.ylabel('Loss')

plt.title('Model Loss over Epochs')

plt.legend()

plt.subplot(1, 2, 2)

plt.plot(history.history['accuracy'], label='Train Accuracy', color='blue')

plt.plot(history.history['val_accuracy'], label='Val Accuracy', color='green')

plt.xlabel('Epoch')

plt.ylabel('Accuracy')

plt.title('Model Accuracy over Epochs')

plt.legend()

plt.tight_layout()

plt.show()

# ---------------------

# 🔍 Prediction Examples

# ---------------------

test_points = np.array([

[1, 1], # Likely Red

[5, 5], # Likely Green

[9, 1.5], # Likely Blue

[4, 4], # Maybe Green

[7, 2.5] # Maybe Blue

])

preds = model.predict(test_points)

pred_labels = encoder.inverse_transform(np.argmax(preds, axis=1))

print("\nPrediction Examples:")

for point, label in zip(test_points, pred_labels):

print(f"Point {point} → Predicted Color: {label}")

במהלך אימון של רשת נוירונים, אנו מודדים שני מדדים חשובים:

אובדן אימון (Training Loss)

אובדן האימון מודד עד כמה המודל מצליח לחזות נכון את הדוגמאות שהוא ראה ולמד מהן בזמן האימון.

ו־אובדן ולידציה (Validation Loss).

אובדן הולידציה מודד את ביצועי המודל על דוגמאות שהוא לא ראה — כלומר, על נתונים שלא היו חלק מהאימון, כדי לבדוק את יכולת ההכללה שלו לעולם האמיתי. אם המודל טוב, שני הערכים אמורים לרדת יחד. אך אם רואים שהאובדן באימון ממשיך לרדת ואילו אובדן הולידציה מתחיל לעלות, זו אינדיקציה לכך שהמודל מתחיל לזכור את הנתונים במקום ללמוד מהם — תופעה שנקראת התאמת יתר (Overfitting). המטרה היא לשמור על איזון בין השניים, כדי שהמודל ילמד טוב אך גם ידע להתמודד עם נתונים חדשים.

רשתות ניירונים – בינה מלאכותית – TensorFlow ANN

תרגיל 2 : בנה רשת ניירונים colab בעזרת בינה מאלכותית TensorFlow עבור הפונקציה 1 משתנה

y=x^2+3

בנה את הפונקציה והצב לה ערכים מ -10 עד 10 בקפיצות של 1
הצג גרף של הפונקציה
בנה רשת בעזרת בינה מלאוכתית אשר מקבל את קלט ופלט ומאמנת את הרשת
בצע פרדיקציה עבור הערכים -2 , -3.45 ,7.45 והצג אותם ערכים לפי הנוסחה וערכים לפי פרדקציה של הרשת

תרגיל 3 : בנה רשת ניירונים colab בעזרת בינה מאלכותית TensorFlow עבור הפונקציה 2 משתנים

בנה את הפונקציה והצב לה ערכים m מ0 עד 10 בקפיצות של 1 , h מ 0 עד 10
הצג גרף של הפונקציה עבור m=2 h=0 to 10
בנה רשת בעזרת בינה מלאוכתית אשר מקבל את קלט ופלט ומאמנת את הרשת
בצע פרדיקציה עבור הערכים m=2 h=0.5 ; m=2 h=2.5

בינה מאלכותית RB108-3 – מבוא לרשתות ניירונים ובינה מלאכותית

חלק א:

העשרה : נתחיל משהו מצחיק – מזכיר SUNO

2 .notebooklm פודקאסט

מה יכולת ה-NotebookLM

איך ניתן שהיא לא תוסיף דברים שלא בחורנו ?

איך היא כן תוסיף עצמה – תכנים אוטומטיים

אפשרות “Auto-Expand”

חלק ב: פיתוח מוצר בעזרת בינה מלאכותית LLM

חלק ג : מבוא רשתות נוירונים (ראשוני)

רשתות ניירונים ANN בינה מלאכותית

פונקציה אקטיבציה : (פועלת על כל ניירון בודד )

1) מה זה MLP

2) קלט (Input) ותכונות (Features)

3) פלט יעד (Targets / Labels)

4) נוירון (Neuron) ומה הוא מחשב

שלב א: חישוב לינארי

שלב ב: אקטיבציה (Activation)

5) שכבת Dense / Fully-Connected

6) שכבות חבויות (Hidden Layers)

7) פונקציית אקטיבציה (Activation Function)

ReLU

8) שכבת פלט (Output Layer) וסוג הבעיה (Regression)

9) פונקציית הפסד (Loss) – MSE

10) אופטימייזר (Optimizer) – Adam

11) Epoch ואימון (Training)

12) חיזוי (Prediction) והכללה (Generalization)

https://colab.research.google.com/drive/1aS5y_LKPePjloHi57PZforMGqOESZGgX?usp=sharing

רשתות ניירונים ANN בינה מלאכותית

במה היא שונה מרשת שחוזה ערך כמו טמפרטורה?

קישור ל ANN – (Artificial Neural Network) classifier

SDR – Software Defined Radio

תרגיל כיתה 2.1 רשת ניירונים חיזוי קטגוריה

רשתות ניירונים – בינה מלאכותית – TensorFlow ANN

תרגיל 2 : בנה רשת ניירונים colab בעזרת בינה מאלכותית TensorFlow עבור הפונקציה 1 משתנה

y=x^2+3

תרגיל 3 : בנה רשת ניירונים colab בעזרת בינה מאלכותית TensorFlow עבור הפונקציה 2 משתנים

אולי תאהב/י גם

RB10 : שיעור -018 זרוע רבוטית

פיתוח אמבדד : esp32

קורס יסודות בינה מלאכותית RB26-08