בלוג

בינה מאלכותית RB14-17 : ניבוי סדרות ורצפים עם בינה מלאכותית LSTM חלק 2

בינה מאלכותית RB14-17 : ניבוי סדרות ורצפים עם בינה מלאכותית LSTM חלק 2

this code generate the  gpraph

Detailed Explanation of the Code

# -*- coding: utf-8 -*-
"""
Generate synthetic ECG signal with NeuroKit2
Plot waveform and frequency spectrum (0–100 Hz)
"""

  • This is just the script header.

  • utf-8 ensures the file supports standard text encoding.

  • The docstring describes what the script does: generate ECG and analyze its spectrum.

Imports

import neurokit2 as nk
import matplotlib.pyplot as plt
import numpy as np

  • neurokit2 (nk): library for biosignal simulation and analysis.

  • matplotlib.pyplot (plt): plotting graphs.

  • numpy (np): numerical operations, arrays, FFT (Fast Fourier Transform).

Step 1 – Generate ECG Signal

fs = 500 # sampling frequency
ecg = nk.ecg_simulate(duration=10, sampling_rate=fs, heart_rate=70)

  • fs = 500: number of samples per second (Hz).

  • nk.ecg_simulate(...): generates a synthetic ECG signal.

    • duration=10 → 10 seconds of data.

    • sampling_rate=500 → 500 samples each second → total 5000 samples.

    • heart_rate=70 → 70 beats per minute (~1.17 Hz).

  • ecg is now a NumPy array of length 5000 containing ECG amplitude values.

Step 2 – Plot Time Domain Signal

plt.figure(figsize=(12,4))
plt.plot(ecg[:2000])
plt.title("Synthetic ECG from NeuroKit2 (first 2000 samples)")
plt.xlabel("Samples")
plt.ylabel("Amplitude")
plt.grid(True)
plt.show()

  • ecg[:2000]: plots only the first 2000 samples (~4 seconds) to zoom in.

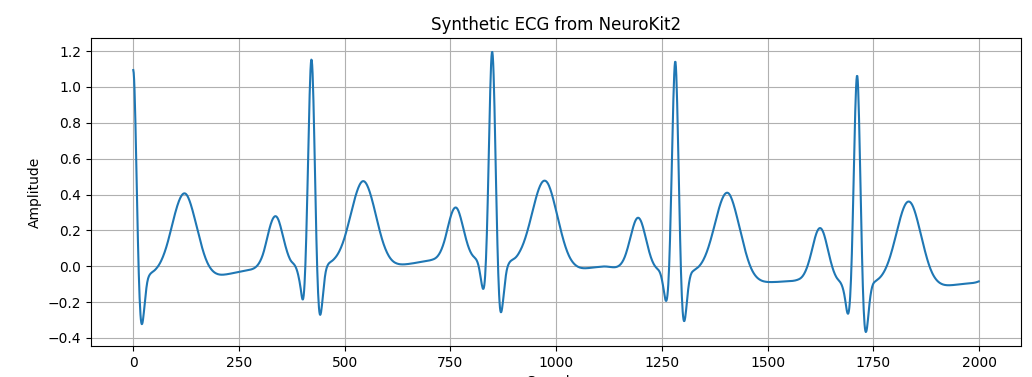
  • The plot shows ECG waveform: repeating cycles with P-wave, QRS complex, and T-wave.

  • figsize=(12,4): wide aspect ratio for clarity.

Step 3 – Frequency Analysis (FFT)

N = len(ecg) # number of samples

  • N = 5000 (10 seconds × 500 samples/second).

fft_vals = np.fft.rfft(ecg) # FFT values (magnitude + phase)
fft_freqs = np.fft.rfftfreq(N, 1/fs) # frequency axis

  • FFT (Fast Fourier Transform) converts time-series → frequency domain.

  • np.fft.rfft → computes FFT only for positive frequencies (saves space).

  • np.fft.rfftfreq(N, 1/fs) → generates the corresponding frequency bins (0 to Nyquist = fs/2 = 250 Hz).

Find Dominant Frequency

idx = np.argmax(np.abs(fft_vals[1:])) + 1
main_freq = fft_freqs[idx]
main_bpm = main_freq * 60

  • np.abs(fft_vals) → magnitude spectrum (ignores phase).

  • [1:] skips index 0 (DC component).

  • np.argmax(...) → index of the frequency with maximum amplitude.

  • main_freq → the dominant frequency (in Hz).

  • main_bpm = main_freq * 60 → converts Hz to beats per minute.

Expected result:

  • Main frequency ≈ 1.17 Hz.

  • Heart rate ≈ 70 bpm (as set in the simulator).

Step 4 – Plot Frequency Spectrum

plt.figure(figsize=(12,4))
plt.plot(fft_freqs, np.abs(fft_vals))
plt.title("Frequency Spectrum of Synthetic ECG (0–100 Hz)")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Magnitude")
plt.grid(True)
plt.xlim(0, 40) # show up to 40 Hz
plt.show()

  • Plots the FFT spectrum: frequency on x-axis, magnitude on y-axis.

  • plt.xlim(0, 40) zooms in to 0–40 Hz (where heart-related frequencies live).

  • You will see:

    • A main peak around 1.17 Hz → corresponds to heartbeat.

    • Smaller harmonics (multiples of 1.17 Hz) due to ECG waveform complexity.

Step 1 – Generate a Synthetic ECG

We use NeuroKit2’s ecg_simulate() function to create a clean ECG waveform.

# -*- coding: utf-8 -*-
"""
Generate synthetic ECG signal with NeuroKit2
and analyze its main frequency content
"""

import neurokit2 as nk
import matplotlib.pyplot as plt
import numpy as np

# Generate synthetic ECG (10 seconds, 500 Hz sampling rate, 70 bpm)
ecg = nk.ecg_simulate(duration=10, sampling_rate=500, heart_rate=70)

  • duration=10 → generate 10 seconds of signal

  • sampling_rate=500 → 500 samples per second

  • heart_rate=70 → target heart rate (70 beats per minute ≈ 1.17 Hz)

At this point, ecg is just a NumPy array with the amplitude values of the simulated ECG signal.

Step 2 – Plot the ECG

We can visualize the waveform and check its shape:

# Plot first 2000 samples (~4 seconds of data)
plt.figure(figsize=(12,4))
plt.plot(ecg[:2000])
plt.title("Synthetic ECG from NeuroKit2 (first 2000 samples)")
plt.xlabel("Samples")
plt.ylabel("Amplitude")
plt.grid(True)
plt.show()

This plot shows the typical ECG waves (P, QRS, T complexes) repeated every heartbeat.

Step 3 – Frequency Analysis with FFT

To find the main repeating pattern in the ECG, we move to the frequency domain using the Fast Fourier Transform (FFT).

# Frequency analysis
fs = 500 # Sampling frequency in Hz
N = len(ecg) # Number of samples

# Apply FFT
fft_vals = np.fft.rfft(ecg) # spectrum values
fft_freqs = np.fft.rfftfreq(N, 1/fs) # corresponding frequencies

# Find dominant frequency (skip DC at index 0)
idx = np.argmax(np.abs(fft_vals[1:])) + 1
main_freq = fft_freqs[idx] # main frequency in Hz
main_bpm = main_freq * 60 # convert to beats per minute

print("Dominant frequency (Hz):", main_freq)
print("Equivalent heart rate (bpm):", main_bpm)

# Plot frequency spectrum
plt.figure(figsize=(12,4))
plt.plot(fft_freqs, np.abs(fft_vals))
plt.title("Frequency spectrum of synthetic ECG")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Magnitude")
plt.grid(True)
plt.xlim(0, 5) # ECG heartbeats usually below 5 Hz
plt.show()

Explanation

  • np.fft.rfft → computes FFT for real-valued signals (positive frequencies only).

  • np.fft.rfftfreq → returns the frequency values for the spectrum.

  • Dominant frequency is found by looking for the largest magnitude peak (excluding DC at 0 Hz).

  • Convert Hz → bpm by multiplying by 60.

For our simulation, the main frequency should be around 1.17 Hz, which equals 70 bpm—the same heart rate we set at the beginning.

Conclusion

With just a few lines of Python:

  1. We generated a synthetic ECG signal.

  2. We plotted and inspected the waveform.

  3. We used FFT to extract its main repeating frequency and confirmed the heart rate.

This workflow demonstrates how to bridge between time domain (ECG waveform) and frequency domain (heart rate and rhythm analysis).

part 2  :

Find the repeated  sequence

line-by-line explanation of your “shifted ECG + repeated sequence overlay” script. I explain every function and parameter used.

# -*- coding: utf-8 -*-
"""
Generate synthetic ECG with NeuroKit2
Shift data by 10 samples
Plot waveform, frequency spectrum, and highlight repeated sequence (heartbeat)
"""

  • Declares UTF-8 source encoding.

  • The docstring summarizes the script’s purpose.

import neurokit2 as nk
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import correlate

  • neurokit2 as nk: toolkit for biosignal simulation/analysis (we’ll use ecg_simulate, ecg_peaks).

  • matplotlib.pyplot as plt: plotting API used for figures/axes (figure, plot, title, etc.).

  • numpy as np: numerical arrays and slicing.

  • scipy.signal.correlate: cross-correlation function (imported here but not used in this snippet; can be removed safely).

1) Generate ECG and shift by 10 samples

fs = 500 # sampling frequency

  • fs: sampling rate in Hz (samples per second). Here 500 Hz.

ecg_full = nk.ecg_simulate(duration=10, sampling_rate=fs, heart_rate=70)

  • nk.ecg_simulate(...) creates a synthetic ECG as a 1-D NumPy array.

  • Parameters:

    • duration=10: total signal duration in seconds → expected length ≈ 10 * fs = 5000 samples.

    • sampling_rate=fs: number of samples per second (here 500).

    • heart_rate=70: target heart rate in bpm (beats per minute). 70 bpm ≈ 1.1667 Hz.

  • Return: ecg_full is the full ECG array (float values).

ecg = ecg_full[10:]

  • Slices the array starting at index 10, effectively shifting the signal by 10 samples (discarding the first 10 points).

  • New length is len(ecg_full) - 10.

print("Original length:", len(ecg_full), "Shifted length:", len(ecg))

  • Prints the number of samples before/after shifting to confirm the 10-sample offset.

2) Detect the repeated sequence (R-peaks)

signals, info = nk.ecg_peaks(ecg, sampling_rate=fs)

  • Detects R-peaks (the tall spikes in QRS complexes) in the shifted ECG.

  • Parameters:

    • ecg: the input ECG array (shifted).

    • sampling_rate=fs: Hz; needed to set internal filter and timing scales.

  • Returns:

    • signals: dict/DataFrame with binary peak annotations (e.g., ECG_R_Peaks series).

    • info: dictionary with indices of detected peaks and metadata. We’ll use info["ECG_R_Peaks"].

rpeaks = info["ECG_R_Peaks"]

  • rpeaks: NumPy array of sample indices (integer positions in ecg) where R-peaks occur.

  • Note: these indices are relative to the shifted series (index 0 is ecg_full[10]).

3) Extract one full heartbeat (the repeated sequence)

start = rpeaks[0]
end = rpeaks[1]

  • Takes the first two R-peaks to define one complete cardiac cycle (R-to-R interval).

  • start: sample index of first R-peak.

  • end: sample index of next R-peak.

  • Assumes at least two peaks were found; for safety in production code, check len(rpeaks) >= 2.

heartbeat = ecg[start:end]

  • Slices the ECG between start (inclusive) and end (exclusive).

  • heartbeat is a 1-cycle waveform (the repeated sequence you want to show).

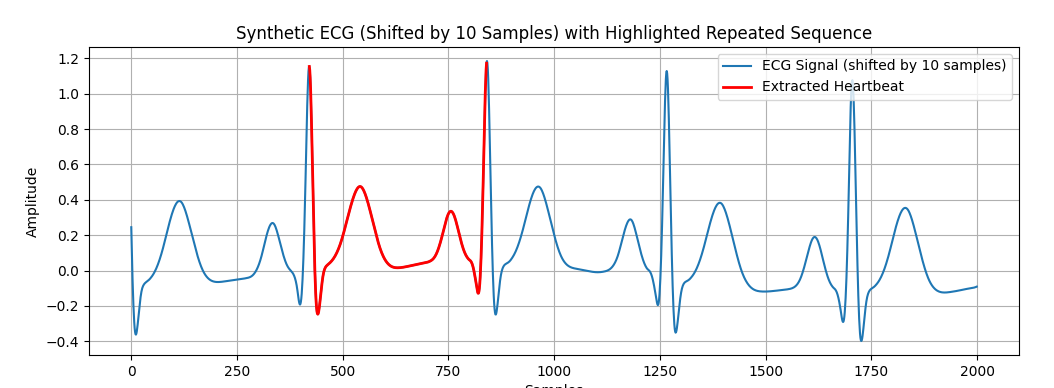
4) Plot the shifted ECG and overlay the extracted heartbeat

plt.figure(figsize=(12,4))

  • Creates a new figure.

  • Parameter:

    • figsize=(12,4): width 12 inches, height 4 inches.

plt.plot(ecg[:2000], label="ECG Signal (shifted by 10 samples)")

  • Plots the first 2000 samples (~4 seconds at 500 Hz) of the shifted ECG.

  • Parameter:

    • label="...": legend entry for this line.

  • The x-axis here is sample index 0..1999 (in the shifted reference frame).

plt.plot(range(start, end), heartbeat, color="red", linewidth=2, label="Extracted Heartbeat")

  • Overlays the extracted heartbeat on the same axes and scale:

    • range(start, end): x-coordinates aligned to the original sample positions within the shifted ECG.
      This ensures the segment appears exactly where it occurs in the larger signal.

    • heartbeat: y-values for that segment.

  • Parameters:

    • color="red": draw the overlay in red.

    • linewidth=2: slightly thicker line for visibility.

    • label="...": legend entry.

plt.title("Synthetic ECG (Shifted by 10 Samples) with Highlighted Repeated Sequence")
plt.xlabel("Samples")
plt.ylabel("Amplitude")
plt.legend()
plt.grid(True)
plt.show()

  • title, xlabel, ylabel: annotate the plot.

  • plt.legend(): shows labels from label= in plot.

  • plt.grid(True): turn on grid lines.

  • plt.show(): renders the figure.

Notes and best practices

  • If ecg_peaks sometimes misses peaks (rare with clean synthetic data), you can fine-tune with method and cleaning parameters in NeuroKit2 (e.g., nk.ecg_clean before peak detection).

  • For robustness, check len(rpeaks) >= 2 before slicing heartbeat.

  • The overlay uses true indices (range(start, end)), so the repeated sequence is displayed on the same scale and at the exact location inside the original graph, as requested.

  • Because you shifted by 10 samples, all indices and plots refer to the shifted signal; the absolute time offset is 10 / fs seconds.

 

 

Explanation of Each Section

1. ECG Generation

ecg_full = nk.ecg_simulate(duration=10, sampling_rate=fs, heart_rate=70)

  • duration=10 → create 10 seconds of ECG data.

  • sampling_rate=500 → 500 samples per second.

  • heart_rate=70 → simulate a heart rate of 70 beats per minute.

We then shift the signal by 10 samples:

ecg = ecg_full[10:]

2. Adding Noise

We define four types of noise:

  • Random Gaussian Noise:

    rand_noise = 0.1 * np.random.randn(len(ecg))

    Simulates random electrical fluctuations.

  • Sinusoidal Drift:

    vig_noise = 0.3 * np.sin(2 * np.pi * 0.5 * t)

    Low-frequency baseline wander (e.g., breathing, electrode motion).

  • Hybrid Noise:

    hybrid_noise = rand_noise + vig_noise

    Combination of the two above.

  • Repeated Noise:

    repeated_noise = 0.15 * np.sin(2 * np.pi * 50 * t)

    Simulates 50 Hz periodic interference (like mains power hum).

3. Create Noisy ECG Variants

Each noisy version is created by adding the noise to the clean ECG:

ecg_random = ecg + rand_noise
ecg_sinus = ecg + vig_noise
ecg_hybrid = ecg + hybrid_noise
ecg_repeated = ecg + repeated_noise

4. Extract the Repeated Sequence

We use NeuroKit2’s ecg_peaks to detect R-peaks:

signals, info = nk.ecg_peaks(signal, sampling_rate=fs)
rpeaks = info["ECG_R_Peaks"]

  • The first two R-peaks define one heartbeat cycle:

start, end = rpeaks[0], rpeaks[1]
heartbeat = signal[start:end]

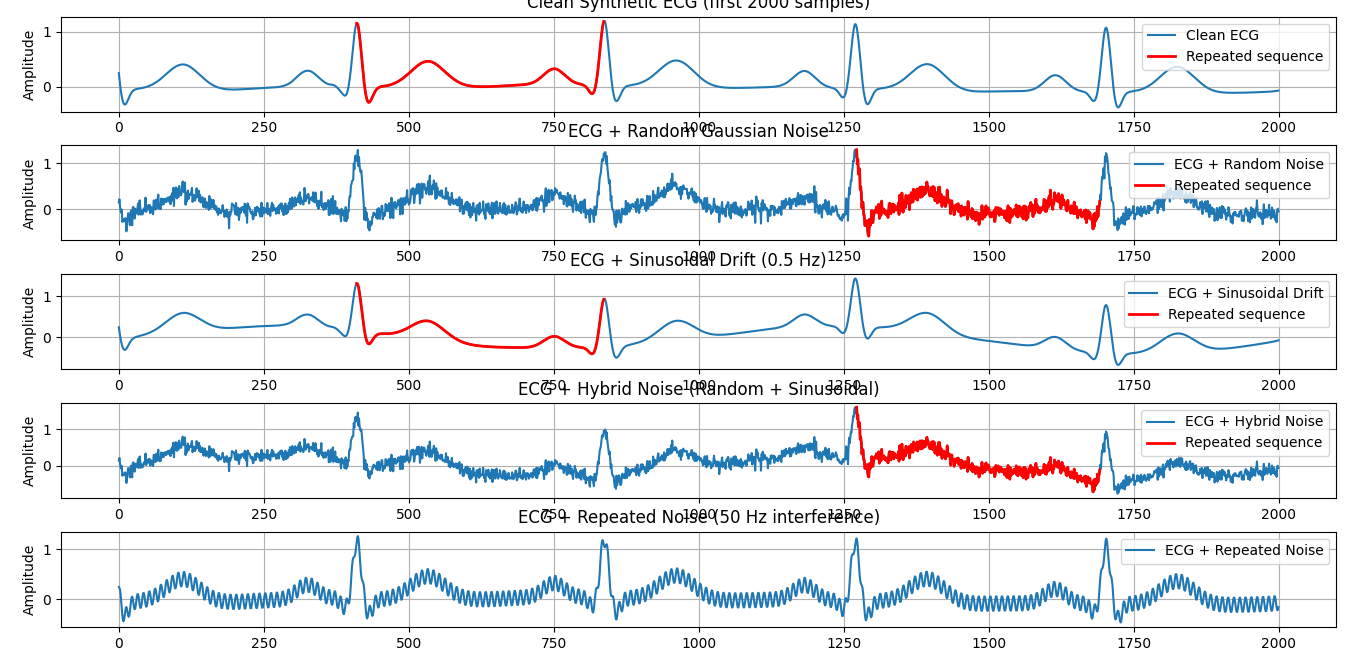
5. Plot Results

We plot 2000 samples (~4 seconds) for each case:

  • Clean ECG

  • ECG + random noise

  • ECG + sinusoidal drift

  • ECG + hybrid noise

  • ECG + repeated noise

On each graph:

  • The full ECG is in blue.

  • The extracted repeated heartbeat cycle is overlaid in red.

Conclusion

This script demonstrates how:

  • Noise affects ECG signals differently.

  • Even with noise, repeated heartbeat cycles can be extracted using R-peak detection.

  • You can simulate realistic ECG scenarios for testing signal-processing algorithms.

כתיבת תגובה